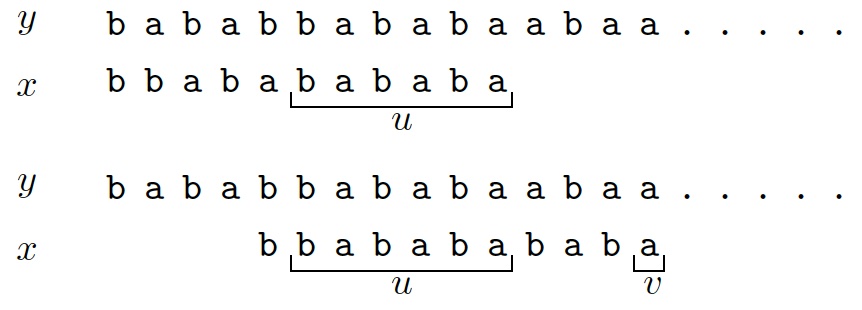CLR cover
Previous problem

Problem 35: Turbo-BM algorithm

Next problem
\( \def\sa#1{\tt{#1}} \def\memo{\mathit{mem}} \def\shift{\mathit{shift}} \def\turb{\mathit{turbo}} \def\tbsuff{\mathit{good\text{-}suff}} \def\lcs{\mathit{lcs}} \def\dd{\dot{}dot{}} \)

The problem shows how a very light modification of Boyer-Moore string matching produces a much faster algorithm when the method is used to locate all the pattern occurrences in a text, like Algorithm BM in Problem 34 does. The initial design of the Boyer-Moore algorithm was to find the first pattern occurrence. It is known that for that goal it runs in linear time with respect to the searched text length. But it has a quadratic worst-case running time to report all pattern occurrences, especially for periodic patterns. This is due to its amnesic aspect when it slides the window to the next position.

The goal of Algorithm Turbo-BM is to get a linear-time search by adapting the Boyer-Moore search algorithm, Algorithm BM, without changing its pattern preprocessing, table $\tbsuff$. Only constant extra space is added and used during the search.

Turbo-BM Algorithm

Algorithm Turbo-BM uses the lengths $\memo=|u|$ of the previous suffix match $u$ and $\ell=|v|$ of the current suffix match $v$ to compute $\max\{\tbsuff[i],|u|-|v|\}$.

In the example below, the first match $u=\sa{bababa}$ of length $6$ leads to a slide of length $4=\tbsuff[4]$. After sliding the window, the new match $v=\sa{a}$ alone would give a slide of length $1=\tbsuff[9]$. But the turbo-shift applies and produces a slide of length $\turb=6-1=5$.

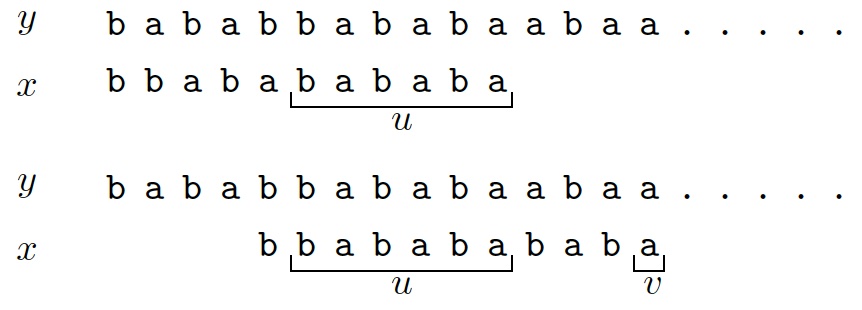
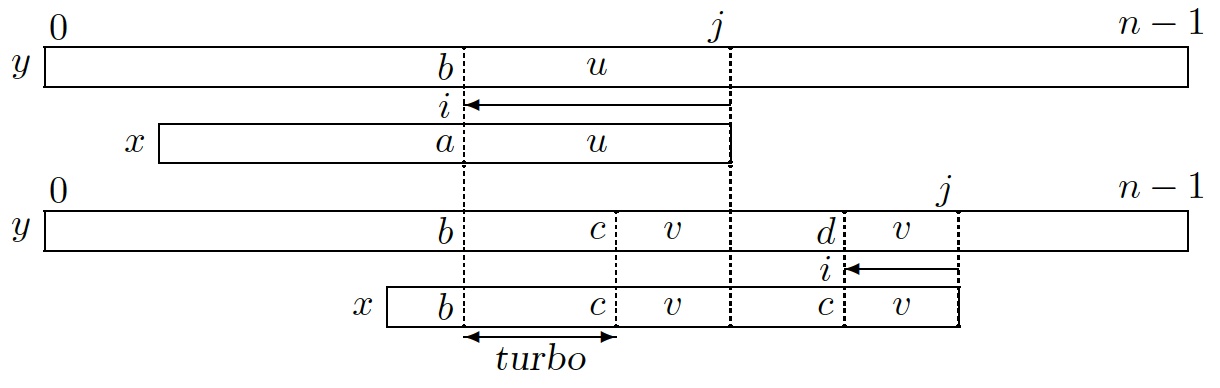
Turbo-BM Algorithm

Show that Algorithm Turbo-BM correctly reports all occurrences of the pattern $x$ in $y$.

Turbo-BM\((x, y \mbox{ non-empty word}, m,n \mbox{ their lengths})\) 
\begin{algorithmic}
  \COMMENT{jumping over memory if $mem \gt 0$}
  \STATE $(j,mem) \leftarrow (m-1,0)$
  \WHILE{$j \lt n$}
    \STATE $i \leftarrow m-1-|lcs(x,y[j-m+1..j])|$
    \IF{$i \lt 0$}
      \STATE report an occurrence of $x$ at position $j-m+1$ on $y$
      \STATE $(shift,\ell) \leftarrow (per(x),m-per(x))$
    \ELSE
      \STATE $(shift,\ell) \leftarrow (good\text{-}suff[i],m-i-1)$
    \ENDIF
    \STATE $turbo \leftarrow mem-(m-i-1)$
    \IF{$turbo\gt shift$}
      \STATE $(j,mem) \leftarrow (j+turbo,0)$
    \ELSE
      \STATE $(j,mem) \leftarrow (j+shift,\ell)$
    \ENDIF
  \ENDWHILE
\end{algorithmic}

References

  • A. Apostolico and R. Giancarlo. The Boyer-Moore-Galil string searching strategies revisited. SIAM J. Comput., 15(1):98-105, 1986.
  • M. Crochemore, A. Czumaj, L. Gasieniec, S. Jarominek, T. Lecroq, W. Plandowski, and W. Rytter. Speeding up two string-matching algorithms. Algorithmica, 12(4/5):247-267, 1994.
  • M. Crochemore, C. Hancart, and T. Lecroq. Algorithms on Strings. Cambridge University Press, 2007. 392 pages.
  • M. Crochemore and T. Lecroq. Tight bounds on the complexity of the Apostolico-Giancarlo algorithm. Inf. Process. Lett., 63(4):195-203, 1997.
  • M. Crochemore and W. Rytter. Text algorithms. Oxford University Press, 1994. 412 pages.
  • Z. Galil. On improving the worse case running time of the Boyer-Moore string matching algorithm. Commun. ACM, 22(9):505-508, 1979.