
|
Remarkable Words
|

|
\(
\def\sa#1{\tt{#1}}
\def\fib{\mathit{fib}}
\def\pgcd{\mathit{gcd}}
\)
Besides Lyndon words, three sets of words have remarkable properties and are
often used in examples.
They are Thue-Morse words, Fibonacci words and de Bruijn words.
The first two are prefixes of (one-way) infinite words.
Formally an infinite word on the alphabet $A$ is a mapping from natural
numbers to $A$.
Their set is denoted by $A^\infty$.
The notion of (monoid) morphism is central to defining some infinite
sets of words or an associate infinite word.
A morphism from $A^*$ to itself (or another free monoid) is a mapping
$h : A^* \mapsto A^*$ satisfying $h(uv)=h(u)h(v)$ for all words $u$ and $v$.
Consequently, a morphism is
entirely defined by the images $h(a)$ of letters $a\in A$.
The Thue-Morse word is produced by iterating the Thue-Morse
morphism $\mu$ from $\{\sa{a}, \sa{b}\}^*$ to itself, defined by
$$\cases{
\mu(\sa{a}) = \sa{ab}, &\cr
\mu(\sa{b}) = \sa{ba}. &\cr
}
$$
Iterating the morphism from letter $\sa{a}$ gives the list of Thue-Morse
words $\mu^k(\sa{a})$, $k\geq 0$, that starts with
$$\begin{array}{lcl}
\tau_0=\mu^0(\sa{a}) & = & \sa{a} \\
\tau_1=\mu^1(\sa{a}) & = & \sa{ab} \\
\tau_2=\mu^2(\sa{a}) & = & \sa{abba} \\
\tau_3=\mu^3(\sa{a}) & = & \sa{abbabaab} \\
\tau_4=\mu^4(\sa{a}) & = & \sa{abbabaabbaababba} \\
\tau_5=\mu^5(\sa{a}) & = & \sa{abbabaabbaababbabaababbaabbabaab}
\end{array}
$$
and eventually produces its infinite associate:
$$\mathbf{t} = \lim_{k \rightarrow \infty}\mu^k(\sa{a}) =
\sa{abbabaabbaababbabaababbaabbabaab}\cdots.
$$
An equivalent definition of Thue-Morse words is provided by the following
recurrence:
$$\cases{
\tau_0 = \sa{a}, \cr
\tau_{k+1} = \tau_k\overline{\tau_k}, & for $k \geq 0$,
}$$
where the bar morphism is defined by
$\overline{\sa{a}}=\sa{b}$ and $\overline{\sa{b}}=\sa{a}$.
Note the length of the $k$th Thue-Morse word is $|\tau_k|=2^k$.
A direct definition of $\mathbf{t}$ is as follows: the letter $\mathbf{t}[n]$
is $\sa{b}$ if the number of occurrences of digit $\sa{1}$ in the binary
representation of $n$ is odd, and is $\sa{a}$ otherwise.
The infinite Thue-Morse word is known to contain no overlap (factor of the
form $auaua$ for a letter $a$ and a word $u$), that is, no factor of exponent
larger than $2$.
It is said to be overlap-free.
The Fibonacci word is similarly produced by iterating a morphism, the
Fibonacci morphism $\phi$ from $\{\sa{a}, \sa{b}\}^*$ to itself, defined
by
$$\cases{
\phi(\sa{a}) = \sa{ab}, &\cr
\phi(\sa{b}) = \sa{a}. &
}
$$
Iterating the morphism from letter $\sa{a}$ gives the list of Fibonacci words
$\phi^k(\sa{a})$, $k\geq 0$, that starts with
$$\begin{array}{lcl}
\fib_0=\phi^0(\sa{a}) & = & \sa{a} \\
\fib_1=\phi^1(\sa{a}) & = & \sa{ab} \\
\fib_2=\phi^2(\sa{a}) & = & \sa{aba} \\
\fib_3=\phi^3(\sa{a}) & = & \sa{abaab} \\
\fib_4=\phi^4(\sa{a}) & = & \sa{abaababa} \\
\fib_5=\phi^5(\sa{a}) & = & \sa{abaababaabaab} \\
\fib_6=\phi^6(\sa{a}) & = & \sa{abaababaabaababaababa}
\end{array}
$$
and eventually its infinite associate:
$$\mathbf{f} = \lim_{k \rightarrow \infty}\phi^k(\sa{a}) =
\sa{abaababaabaababaababaabaababaabaab}\cdots.$$
An equivalent definition of Fibonacci words comes from the recurrence
relation:
$$\cases{
\fib_0 = \sa{a}, \cr
\fib_1 = \sa{ab}, \cr
\fib_{k+1} = \fib_{k}\fib_{k-1}, & for $k \geq 1$.
}$$
The sequence of lengths of these words is the sequence of Fibonacci numbers,
that is, $|\fib_k|=F_{k+2}$.
Recall that Fibonacci numbers are defined by the recurrence
$$\cases{
F_0 = 0, \cr
F_1 = 1, \cr
F_{k+1} = F_k+F_{k-1}, & for $k \geq 1$.
}$$
Among many properties they satisfy are
-
$\pgcd(F_n,F_{n-1})=1$, for $n\geq 2$,
-
$F_n$ is the nearest integer of $\Phi^n/\sqrt5$, where
$\Phi=\frac12(1+\sqrt5)=1.61803\cdots$ is the
golden ratio.
The interest in Fibonacci words comes from the combinatorial properties they
satisfy and the large number of repeats they contain.
However, the infinite Fibonacci word contains no factor of exponent larger than
$\Phi^2+1=3.61803\cdots$.
De Bruijn words are defined here on the alphabet
$A=\{\sa a,\sa b\}$ and are parameterised by a positive integer $k$.
A word $x\in A^+$ is a de Bruijn word of order $k$ if each word of $A^k$ occurs
exactly once in $x$.
As a first example, $\sa{ab}$ and $\sa{ba}$ are the only two de Bruijn words of
order $1$.
As a second example, the word $\sa{aaababbbaa}$ is a de Bruijn word of order $3$,
since its eight factors of length 3 are the eight words of $A^3$, that is,
$\sa{aaa}$, $\sa{aab}$, $\sa{aba}$, $\sa{abb}$, $\sa{baa}$, $\sa{bab}$,
$\sa{bba}$ and $\sa{bbb}$.
The existence of a de Bruijn word of order $k\geq2$ can be verified with the
help of the de Bruijn automaton defined by
-
States are the words of $A^{k-1}$.
-
Arcs are of the form $(av,b,vb)$ with $a,b\in A$ and $v\in A^{k-2}$.
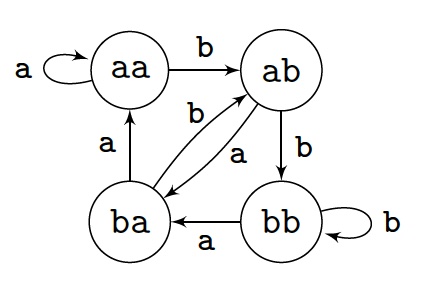
The picture displays the automaton for de Bruijn words of order $3$.
Note that exactly two arcs exit each of the states, one labelled by $\sa a$,
the other by $\sa b$; and that exactly two arcs enter each of the states, both
labelled by the same letter.
The graph associated with the automaton thus satisfies the Euler condition:
every vertex has an even degree.
It follows that there exists an Eulerian circuit in the graph.
Its label is a
circular de Bruijn word.
Appending to it its prefix of length $k-1$ gives an ordinary de Bruijn word.
It can also be verified that the number of de Bruijn words of order $k$ is
exponential in $k$.
De Bruijn words can be defined on larger alphabets and are often used as
examples of limit cases because they contain all the factors of a given
length.



