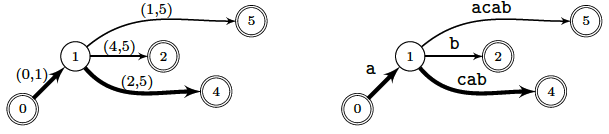Example
\(
\def\sa#1{\tt{#1}}
\def\dd{\dot{}\dot{}}
\def\SA{\mathrm{SA}}
\def\LCP{\mathrm{LCP}}
\)
Here are tables $\SA$ and $\LCP$ of the Suffix array of $\sa{aacab}$:
\[\begin{array}{cccl}
r & \SA & \LCP \cr
\hline
0 & 0 & 0 & \sa{aacab} \cr
1 & 3 & 1 & \sa{ab} \cr
2 & 1 & 1 & \sa{acab} \cr
3 & 4 & 0 & \sa{b} \cr
4 & 2 & 0 & \sa{cab}
\end{array}\]
Table $\SA$ stores the starting position of non-empty suffixes according
to their rank $r$ in lexicographic order.
Suffixes themselves are not part of the structure.
Table $\LCP[r]$ gives the longest common prefix between rank-$r$ and
rank-$(r-1)$ suffixes.
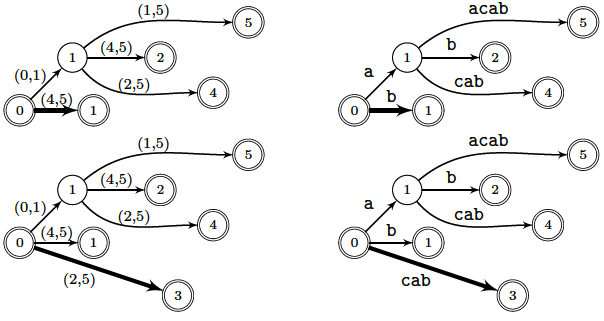
The pictures below illustrate three first steps of a possible Suffix tree
construction for the example $\sa{aacab}$.
The first picture is when suffixes $\sa{aacab}$, $\sa{ab}$ and $\sa{acab}$
have been treated.
Labels of nodes are their word depth and labels of arcs are in the form
$(i,j)$ (on the left) representing factors $x[i\dd j-1]$ (on the right)
of the word $x$.
Doubly circled nodes are terminal states and thick paths show last inserted
suffixes.
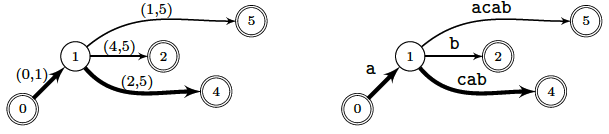

|
Problem 47: Suffix Array to the Suffix Tree
|

|
The goal of the problem is to transform the Suffix array of a word $x$ into
its Suffix tree.
Despite the fact that both data structures infer essentially the same types
of indexing operations, some come more readily from the Suffix
tree structure.
The interest in designing a linear-time algorithm to do it is interesting
when the alphabet is linearly sortable.
Indeed, with this hypothesis, there are many linear-time algorithms to
build the Suffix array of a word, although
there is mostly one method to build its Suffix tree in the same time.
Moreover, techniques used for the former construction are way easier to
develop.
Show how to build the Suffix tree of a word in linear time given its Suffix array.
References
M. Crochemore, C. Hancart, and T. Lecroq. Algorithms on Strings.
Cambridge University Press, 2007. 392 pages.
M. Farach. Optimal suffix tree construction with large alphabets. In
38th Annual Symposium on Foundations of Computer Science, FOCS
'97, Miami Beach, Florida, USA, October 19-22, 1997, pages 137-143.
IEEE Computer Society, 1997.
J. Kärkkäinen and P. Sanders. Simple linear work suffix array construction.
In J. C. M. Baeten, J. K. Lenstra, J. Parrow, and G. J. Woeginger,
editors, Automata, Languages and Programming, 30th International
Colloquium, ICALP 2003, Eindhoven, The Netherlands, June 30
- July 4, 2003. Proceedings, volume 2719 of Lecture Notes in Computer
Science, pages 943-955. Springer, 2003.
J. Kärkkäinen, P. Sanders, and S. Burkhardt. Linear work suffix array
construction. J. ACM, 53(6):918-936, 2006.
D. K. Kim, J. S. Sim, H. Park, and K. Park. Constructing suffix arrays
in linear time. J. Discrete Algorithms, 3(2-4):126-142, 2005.
P. Ko and S. Aluru. Space efficient linear time construction of suffix
arrays. J. Discrete Algorithms, 3(2-4):143-156, 2005.