Example

$ \def\sa#1{\tt{#1}} \def\dd{\dot{}\dot{}} \newcommand{\hufflabel}{\mathit{label}}% \newcommand{\alph}{\mathit{alph}}% \newcommand{\freq}{\mathit{freq}}% \newcommand{\code}{\mathit{code}}% \newcommand{\result}{\mathit{result}}% $

Let $S=\{7,1,3,1\}$. Initially $\result=0$.
Step 1: $p=1$, $q=1$, $p+q=2$, $S=\{7,3,2\}$, $\result=2$.
Step 2: $p=2$, $q=3$, $p+q=5$, $S=\{7,5\}$, $\result=7$.
Step 3: $p=5$, $q=7$, $p+q=12$, $S=\{12\}$, $\result=19$.

The Huffman forest underlying the algorithm, which ends up with a Huffman tree, is shown in the picture. Nodes are labelled with weights.

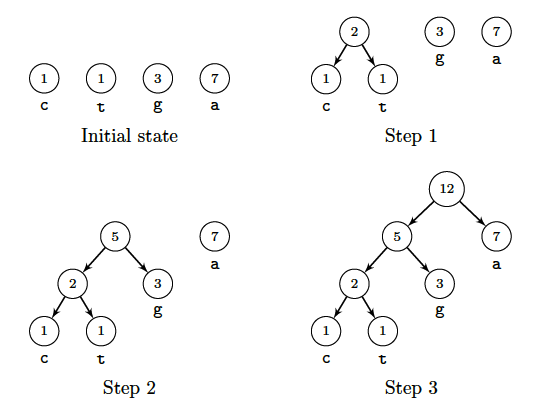
The final tree provides codewords associated with letters, summarised in the table.

	$\sa{a}$	$\sa{c}$	$\sa{g}$	$\sa{t}$
$\freq$	7	1	3	1
$\code$	$\sa{1}$	$\sa{000}$	$\sa{01}$	$\sa{001}$
$\|\code\|$	1	3	2	3

The cost of the tree is $7\times 1 + 1\times 3 + 3\times 2 + 1\times 3=19$. It is the length of the compressed word $\sa{000}\;\sa{1}\;\sa{01}\;\sa{1}\;\sa{001}\;\sa{1}\;\sa{1}\;\sa{01}\;\sa{1} \;\sa{01}\;\sa{1}\;\sa{1}$ corresponding to \sa{cagataagagaa}, whose letter frequencies fit with those of the example. Encoded with 8-bit codewords, the length of the latter word is $96$.

Problem 99: Cost of a Huffman Code

Huffman compression method applied to a text $x\in A^*$ assigns a binary codeword to each letter of $x$ in order to produce a shortest encoded text. Its principle is that the most frequent letters are given the shortest codewords while the least frequent symbols correspond to the longest codewords.

Codewords form a prefix code (prefix-free set) naturally associated with a binary tree in which the links from a node to its left and right children are labelled by $\sa{0}$ and $\sa{1}$ respectively. Leaves correspond to original letters and labels of branches are their codewords. In the present method codes are complete: internal nodes of the tree all have exactly two children.

The cost of a Huffman code is the sum $\sum_{a\in A} \freq(a) \times |\code(a)|$, where $\code(a)$ is the binary codeword of letter $a$. It is the smallest length of a binary text compressed by the method from a word $x$ in which $\freq(a)=|x|_a$ for each letter $a\in\alph(x)$. Let us consider the following algorithm applied to frequencies (weights).

HuffmanCost$(S \textrm{ list of positive weights})$

    \begin{algorithmic}
  \STATE $result\leftarrow 0$
  \WHILE{$|S|\gt 1$}
    \STATE $p\leftarrow$ MinDelete$(S)$
    \STATE $q\leftarrow$ MinDelete$(S)$
    \STATE add $p+q$ to $S$
    \STATE $result\leftarrow result+p+q$
  \ENDWHILE
  \RETURN{result}
    \end{algorithmic}

Prove that Algorithm HuffmanCost$(S)$ computes the smallest cost of a Huffman code from a list $S$ of item weights.

Consider the Huffman tree associated with the code/

Show how to implement algorithm HuffmanCost$(S)$ so that it runs in linear time when the list $S$ is in increasing order.

Use a queue for inserting the new values (corresponding to internal nodes of the tree).

References

D. A. Huffman. A method for the construction of minimum redundancy codes. Proc. I.R.E., 40:1098-1101, 1951.

J. van Leeuwen. On the construction of Huffman trees. In ICALP, pages 382-410, 1976.

125 Problems in Text Algorithms

Example

Problem 99: Cost of a Huffman Code

References