Example
\(
\def\sa#1{\tt{#1}}
\def\dd{\dot{}\dot{}}
\def\BWT{\mathrm{BW}}
\)
The factorisation of the word $\sa{abaabababaaababb}$ is
$\sa{a}\cdot\sa{b}\cdot\sa{a}\cdot\sa{aba}\cdot\sa{baba}\cdot\sa{aabab}\cdot\sa{b}$.
For the example word $\sa{banana}$, rotations are listed below on the left
and their sorted list on the right.
Then $\BWT(\sa{banana})=\sa{nnbaaa}$.
| $\scriptsize{0}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ |
| $\scriptsize{1}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ |
| $\scriptsize{2}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ |
| $\scriptsize{3}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ |
| $\scriptsize{4}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ |
| $\scriptsize{5}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ |
|
|
|
| $\scriptsize{5}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ |
| $\scriptsize{3}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ |
| $\scriptsize{1}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ |
| $\scriptsize{0}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ |
| $\scriptsize{4}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ |
| $\scriptsize{2}$ | $\sa{n}$ | $\sa{a}$ | $\sa{n}$ | $\sa{a}$ | $\sa{b}$ | $\sa{a}$ |
|
To do it on $\sa{nnbaaa}$ from the above example, we first sort the letters
getting the word $\sa{aaabnn}$.
Knowing that the first letter of the initial
word appears at position $2$ on $\sa{nnbaaa}$, we can start the decoding: the
first letter is $\sa{b}$ followed by letter $\sa{a}$ at the same position $2$
on $\sa{aaabnn}$.
This is the third occurrence of $\sa{a}$ in $\sa{aaabnn}$
corresponding to its third occurrence in $\sa{nnbaaa}$, which is followed by
$\sa{n}$, and so on.
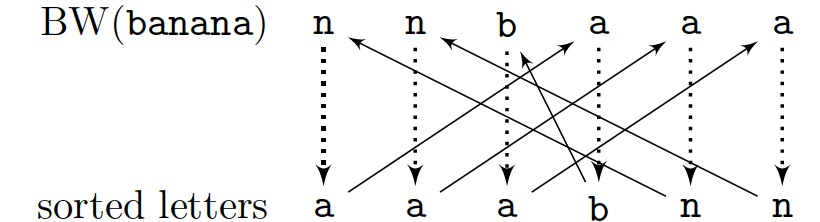
The decoding process is similar to following the cycle in the graph below
from the correct letter.
Starting from a different letter produces a conjugate of the initial word.

|
Compression
|

|
The most powerful compression methods for general
texts are based either on the Ziv-Lempel factorisation of words or on easier
techniques on top of the Burrows-Wheeler transform of words.
We give a glimpse of both.
When processing a word online, the goal of Ziv-Lempel compression
scheme is to capture information that has been met before.
The associated factorisation of a word $x$ is $u_0u_1\cdots u_k$, where $u_i$
is the longest prefix of $u_i\cdots u_k$ that appears before this occurrence
in $x$.
When it is empty, the first letter of $u_i\cdots u_k$, which does not occur in
$u_0\cdots u_{i-1}$, is chosen.
The factor $u_i$ is sometimes called abusively the longest previous
factor at position $|u_0\cdots u_{i-1}|$ on $x$.
There are several variations to define the factors of the decomposition, here
are a few of them.
The factor $u_i$ may include the letter immediately
following the occurrence of the longest previous factor at position
$|u_0\cdots u_{i-1}|$, which amounts to extending a factor occurring before.
Previous occurrences of factors may be chosen among the factors $u_0$, \dots,
$u_{i-1}$ or among all the factors of $u_0\cdots u_{i-1}$ (to avoid an
overlap between occurrences) or among all factors occurring before.
This results in a large variety of text compression software based on the method.
When designing word algorithms the factorisation is also used to reduce some
online processing by storing what has already been done on previous
occurrences of factors.
The Burrows-Wheeler transform of a word
$x$ is a reversible mapping that transforms $x\in A^k$ into
$\BWT(x)\in A^k$.
The effect is mostly to group together letters having the same context in $x$.
The encoding proceeds as follows.
Let us consider the sorted list of rotations (conjugates) of $x$.
Then $\BWT(x)$ is the word composed of the last letters of sorted rotations,
referred to as the last column of the corresponding table.
Two conjugate words have the same image by the mapping.
Choosing the Lyndon word as a representative of the class of a
primitive word, the mapping becomes bijective.
To recover the original word $x$ other than a Lyndon word,
it is sufficient to keep the position on $\BWT(x)$ of the first letter of
$x$.
The main property of the transformation is that occurrences of a given letter
are in the same relative order in $\BWT(x)$ and in the sorted list of all
letters.
This is used to decode $\BWT(x)$.



