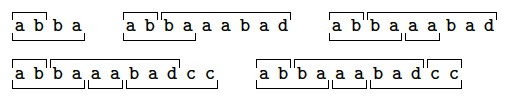Example
\(
\def\sa#1{\tt{#1}}
\def\dd{\dot{}\dot{}}
\)
The set $C_0=\{\sa{ab},\sa{abba},\sa{baccab},\sa{cc}\}$ is not a code because
the word $\sa{abbaccab}\in C_0^*$ has two factorisations,
$\sa{ab}\cdot\sa{baccab}$ and $\sa{abba}\cdot\sa{cc}\cdot\sa{ab}$, on the
words of $C_0$.
On the contrary, the set $C_1=\{\sa{ab},\sa{bacc},\sa{cc}\}$
is a code because a word in $C_1^*$ can start by only one word in $C_1$.
It is said to be a prefix code (no $u\in C$ is a proper prefix of $v\in C$).
To test if $C_2=\{\sa{ab}, \sa{abba}, \sa{baaabad}, \sa{aa}, \sa{badcc},
\sa{cc}, \sa{dccbad}, \sa{badba}\}$ is a code we can try to build a word in
$C_2^*$ with a double factorisation.
Here is a sequence of attempts:
At each step we get a remainder, namely $\sa{ba}$, $\sa{aabad}$,
$\sa{bad}$ and $\sa{cc}$, that we try to eliminate.
Eventually we get a double factorisation because the last remainder
is the empty word.
Then $C_2$ is not a code.

|
Problem 52: Codicity Test
|

|
Sets of words, especially binary words, are used to encode information.
They may be related to transmission protocols, to data compression or mere texts.
Streams of data need to be parsed according to the set to retrieve the
original information.
Parsing is a simple operation when codewords have the
same length, like ASCII and UTF-32 codes for characters, and gives a unique
factorisation of encoded data.
A code is a set of words that features a uniquely decipherable property.
The question of having a unique parsing concerns mostly variable-length codes.
The goal of the problem is to test whether a set of words is a code.
More precisely, a set $C=\{w_1,w_2,\dots,w_n\}$ of words drawn from an alphabet
$A$ is a code if for every two sequences (noted as words)
$i_1i_2\cdots i_k$ and $j_1j_2\cdots j_\ell$ of indices from
$\{1,2,\dots,n\}$ we have
$$i_1i_2\cdots i_k \neq j_1j_2\cdots j_\ell \;\Rightarrow \;
w_{i_1}w_{i_2}\cdots w_{i_k} \neq w_{j_1}w_{j_2}\cdots w_{j_\ell}.$$
In other words, if we define the morphism $h$ from $\{1,2,\dots,n\}^*$ to $A^*$
by $h(i)=w_i$, for $i\in \{1,2,....n\}$, the condition means $h$ is
injective.
The size $N$ of the codicity testing problem for a finite set of words
is the total length $||C||$ of all words of $C$.
Design an algorithm that checks if a finite set $C$ of words is a code
and that runs in time $O(N^2)$.
References
A. Apostolico and R. Giancarlo. Pattern matching machine implementation
of a fast test for unique decipherability. Inf. Process. Lett.,
18(3):155-158, 1984.
J. Berstel and D. Perrin. Theory of Codes. Academic Press, INC.,
Orlando, Florida, 1985.
M. Lothaire. Combinatorics on Words. Addison-Wesley, 1983. Reprinted
in 1997.
A. A. Sardinas and G. W. Patterson. A necessary and sufficient condition
for the unique decomposition of coded messages. Research Division
Report 50-27, Moore School of Electrical Engineering, University of
Pennsylvania, 1950.