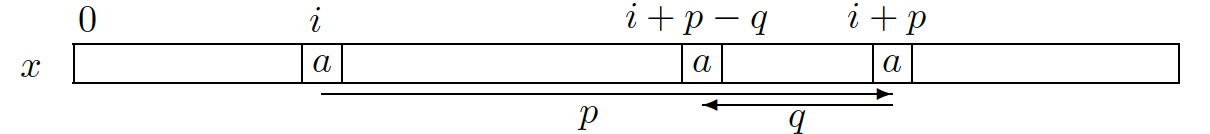Example
\(
\def\sa#1{\tt{#1}}
\def\per{\mathit{per}}
\def\Bord{\mathit{Border}}
\def\mv{\varepsilon}
\def\dd{\dot{}\dot{}}
\def\pgcd{\mathit{gcd}}
\)
3, 6, 7 and 8 are periods of the word $\sa{aabaabaa}$,
and $\per(\sa{aabaabaa})=3$.
$\mv$, $\sa{a}$, $\sa{aa}$, and $\sa{aabaa}$ are the borders of
$\sa{aabaabaa}$ and $\Bord(\sa{aabaabaa})=\sa{aabaa}$.

|
Periodicity
|

|
Let $x$ be a non-empty word. An integer $p$, $0\lt p\leq|x|$, is called a
period of $x$ if $x[i]=x[i+p]$ for $i=0,1,\dots,|x|-p-1$.
Note that the length of a word is a period of this word, so every non-empty
word has at least one period.
The period of $x$, denoted by $\per(x)$, is its smallest period.
Note that if $p$ is a period of $x$, its multiples not larger than $|x|$
are also periods of $x$.
Here is a series of properties equivalent to the definition of a period $p$
of $x$.
First, $x$ can be factorised uniquely as $(uv)^k u$, where $u$ and
$v$ are words, $v$ is non-empty, $k$ is a positive integer and $p=|uv|$.
Second, $x$ is a prefix of $ux$ for a word $u$ of length $p$.
Third, $x$ is a factor of $u^k$, where $u$ is a word of length $p$ and $k$ a
positive integer.
Fourth, $x$ can be factorised as $uw=wv$ for three words $u$, $v$
and $w$, verifying $p=|u|=|v|$.
The last point leads to the notion of border.
A border of $x$ is a proper factor of $x$ that is both a prefix and a suffix of $x$.
The border of $x$, denoted by $\Bord(x)$, is its longest border.
Borders and periods of $x$ are in one-to-one correspondence because of the
fourth point above: a period $p$ of $x$ is associated with the border
$x[p\dd |x|-1]$.
Note that, when defined, the border of a border of $x$ is also a border of $x$.
Then $\langle \Bord(x), \Bord^2(x), \dots, \Bord^k(x)=\mv \rangle$ is
the list of all borders of $x$.
The (non-empty) word $x$ is said to be border free if its only border
is the empty word or equivalently if its only period is $|x|$.
Lemma 1 (Periodicity lemma}
If $p$ and $q$ are periods of a word $x$ and satisfy $p+q-\pgcd(p,q)\leq|x|$
then $\pgcd(p,q)$ is also a period of $x$.
The proof of the lemma may be found in textbooks.
The Weak Periodicity lemma refers to a variant of the lemma in which the condition is
strengthened to $p+q\leq|x|$.
Its proof comes readily as follows.
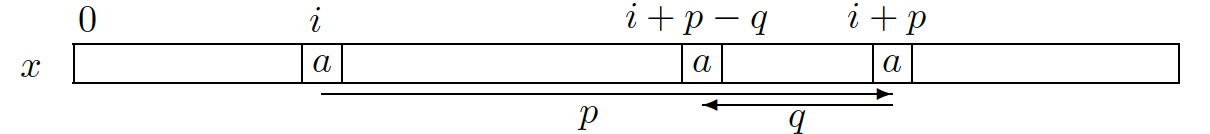
The conclusion obviously holds when $p=q$.
Else, w.l.o.g. assume $p\gt q$ and let us show first that $p-q$ is a period of $x$.
Indeed, let $i$ be a position on $x$ for which $i+p\lt |x|$.
Then $x[i]=x[i+p]=x[i+p-q]$ because $p$ and $q$ are periods.
And if $i+p\geq|x|$, the condition implies $i-q\geq 0$.
Then $x[i]=x[i-q]=x[i+p-q]$ as before.
Thus $p-q$ is a period of $x$.
Iterating the reasoning or using a recurrence as for Euclid's algorithm, we
conclude that $\pgcd(p,q)$ is a period of $x$.
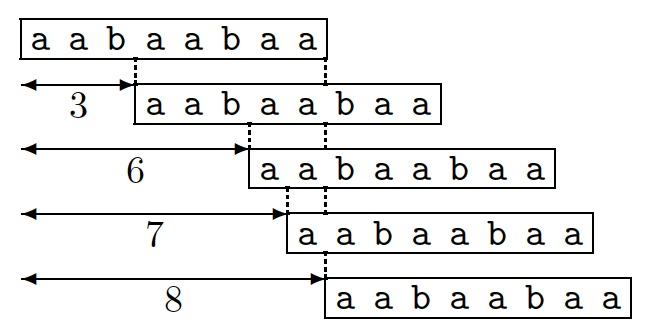
To illustrate the Periodicity lemma, let us consider a word $x$ that admits
5 and 8 as periods.
Then, if we assume moreover that $x$ is composed of at
least two distinct letters, $\pgcd(5,8)=1$ is not a period of $x$.
Thus, the condition of the lemma cannot hold, that is, $|x|\lt 5+8-\pgcd(5,8)=12$.
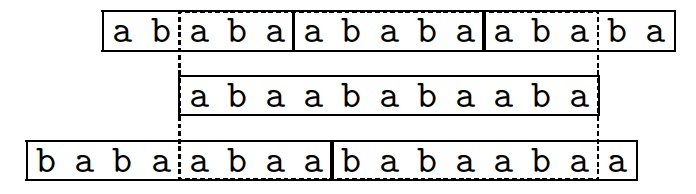
The extreme situation is displayed in the picture and shows (when
generalised) that the condition required on periods in the statement of the
Periodicity lemma cannot be weakened.