
|
Problem 51: Subsequence Automaton
|

|
\(
\def\sa#1{\tt{#1}}
\def\dd{\dot{}\dot{}}
\def\aSMot{\mathcal{SM}}
\)
Subsequences (or subwords) occurring in a word are useful elements to filter
series of texts or to compare them.
The basic data structure for developing applications related to subsequences
is an automaton accepting them due to its reasonable size.
For a non-empty word $y$, let $\aSMot(y)$ be the minimal (deterministic)
automaton accepting the subsequences of $y$.
It is also called the Deterministic Acyclic Subsequence Graph (DASG).
Below is the subsequence automaton of $\sa{abcabba}$.
All its states are terminal and it accepts the set
$$\{\sa{a},\sa{b},\sa{c},\sa{aa},\sa{ab},\sa{ac},
\sa{ba},\sa{bb},\sa{bc},\sa{ca},\sa{cb},\sa{aaa},
\sa{aab},\sa{aba},\sa{abb},\sa{abc},\dots\}.$$
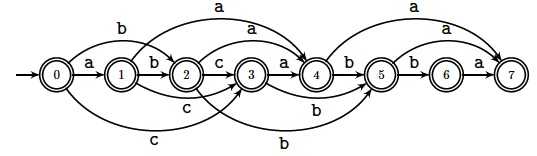
Show how to build the subsequence automaton of a word and analyse the time
and space complexity of the construction according to the size of the
automaton.
Subsequence automata are an essential structure to find words that
discriminate two words because they provide a direct access to all their
subsequences.
A word $u$ distinguishes two distinct words $y$ and $z$ if it
is a subsequence of only one of them, that is, if it is in the symmetric
difference of their associated sets of subsequences.
Show how to compute a shortest subsequence distinguishing two different words
$y$ and $z$ with the help of their automata $\aSMot(y)$ and $\aSMot(z)$.
To design the algorithm it is interesting to note the following property of
the subsequence automaton of $y$: if there is a path from state $0$ to state
$i$ labelled by the word $u$, then $y[0\dd i-1]$ is the shortest prefix of
$y$ containing $u$ as a subsequence.
References
A. V. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis
of Computer Algorithms. Addison-Wesley, 1974.
R. A. Baeza-Yates. Searching subsequences. Theor. Comput. Sci.,
78(2):363-376, 1991.
T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction
to Algorithms, 3rd Edition. MIT Press, 2009.
M. Crochemore and Z. Tronicek. On the size of DASG for multiple
texts. In A. H. F. Laender and A. L. Oliveira, editors, String Processing
and Information Retrieval, 9th International Symposium, SPIRE 2002,
Lisbon, Portugal, September 11-13, 2002, Proceedings, volume 2476 of
Lecture Notes in Computer Science, pages 58-64. Springer, 2002.
Z. Tronicek and B. Melichar. Directed acyclic subsequence graph. In
J. Holub and M. Simánek, editors, Proceedings of the Prague Stringology
Club Workshop 1998, Prague, Czech Republic, September 3-4, 1998,
pages 107-118. Department of Computer Science and Engineering, Faculty
of Electrical Engineering, Czech Technical University, 1998.
Z. Tronicek and A. Shinohara. The size of subsequence automaton.
Theor. Comput. Sci., 341(1-3):379-384, 2005.



